Some math equations simply don’t work. If you ask Siri (iPhone voice assistant), “What is zero divided by zero?” you get a rather funny, yet intriguing response. So ask Siri that question, grab a holiday cookie (makes more sense after asking Siri), and let’s dive into how low rates are impacting some of the mathematical computations long relied on by the municipal bond market (and other markets with optionality).
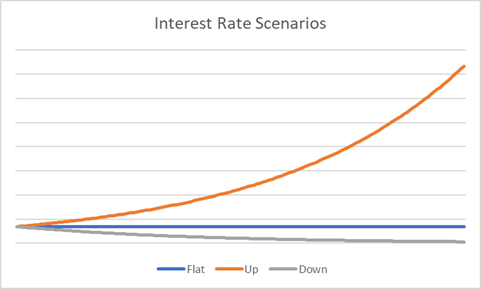
Interest rates can go up, remain flat, or go down, which I realize is not the most brilliant statement ever. What if the mathematical models historically used for option pricing can only value two of these three scenarios? Option Adjusted Spread (OAS) is designed with positive rates in mind, using incremental binomial distributions of above-zero interest rate moves to determine an option’s value. In its simplest form, this option value is either added to (bondholder-friendly option) or subtracted from (issuer-friendly option) an option-free bond to arrive at the total bond value. If rates are incredibly low, you only have so many allowable downward rate moves before reaching zero, but have a limitless upward potential. In better mathematical nomenclature, you have a near-parabolic upside in rate possibilities, but limited downside due to the near-zero asymptote. This is illustrated in the simplified graph below. While there are three interest rate scenarios, the magnitude of the upward move combined with the downside-limiting zero asymptote only allows for meaningful one-way option adjustments. This is problematic, as a callable muni’s option (which belongs to the issuer) has value that grows (further detracting from the bond’s value) with rate moves in either direction. A callable muni bond’s OAS may be overstated in these interest rate scenarios – given its negative convexity and likelihood of being called – as the entire two-way option adjustment detraction is only fully captured in directionally upward rate moves.
A municipal bond’s call option value should reflect both extension and contraction risk. Given the market’s “unique” use of 5% coupons for most bonds (get ready for a future tax-related blog post on this topic – a diatribe against arcane and unnecessary tax policy that is best enjoyed with another cookie; it will make more sense then), let’s assume all bonds for this discussion are high quality, long callables at large premiums (5% coupons vs near 1% yields). As yields rise, the bond’s Option Adjusted Duration (OAD, or just duration) will extend, which is extension risk. The likelihood of the bond being called is reduced, so it could be outstanding longer and therefore have an increasing duration. If yields decline, the call is more likely to be exercised and the duration with shorten, which is contraction risk. The impact to the investor cuts both ways. If yields climb, you will potentially get your principal back later, and be unable to invest at the new, higher prevailing yields. If rates fall, you will get your principal back sooner, and will have to reinvest at the new, lower yields. Both are poor outcomes and represent why the value of the option must be appropriately valued to arrive at fair value.
As we’ve discussed in previous posts, valuations can often require multiple approaches, since sometimes, a single approach can produce false signals. With the mosaic approach to valuation, art and science are combined and appropriately honed from experience, challenging the market status quo. The callable security will have a higher yield than the bullet bond of the same duration. This is the compensation for the negative convexity resulting from the issuer holding the option. The question simply becomes whether this compensation is sufficient. OAS is a good starting point, but many limitations exist, several of which are noted above. As volatility can increase the value of the option and therefore decrease the value of the bond, it is important to optimize – not avoid – this risk in the portfolio. Since nearly 70% of the broad municipal market is callable, avoiding this risk leaves a lot of cheap bonds on the table, and ignoring it leaves investors exposed to the whims of volatility. At IR+M, we feel we have developed the tools and knowledge to appropriately value and optimize the risk of these convexity-related duration moves. We recognize that the answer is not to avoid or ignore the risk, but to optimize it.
So, while zero divided by zero may not make much sense, option pricing can still work with the introduction of a few new approaches.


