Me: “Did you hear about Master Jedi Mace?”
Tired 7-year-old son: “No, what?”
Me: “He fell out the Windu.”
Tired and now angry 7-year-old son: “You woke me up for this?”
This was how my son’s Saturday morning started last week. Personally, I was quite proud to start the day with a (borrowed) Star Wars dad joke. He, at the time, was less impressed. In his defense, it was 6:45am. For anyone who is not a Star Wars fan, Master Jedi Mace Windu (Samuel L. Jackson) died* falling out a window after he was struck by force lightning from Palpatine in Episode III. And if you can’t tell, as a family, we are huge fans of Star Wars.
I love a good dad joke. So much so that for Christmas, my son got me a book of dad jokes (which he now greatly regrets). I even used to tell dad jokes before I was a dad. I guess you could have called me a faux pa.
Ok, ok, so what does this have to do with convexity? Well, dad jokes make people roll their eyes think. Similarly, explanations of convexity often make people think and then they’re more confused than before hearing the explanation. Einstein said, “If you can’t explain it simply, you don’t understand it well enough.” The idea for this piece was generated after I listened to one of our mortgage traders give a presentation on the TBA (to be announced) market, which highlighted its many small nuances, but in a manner that made it understandable. He truly is a subject matter expert.
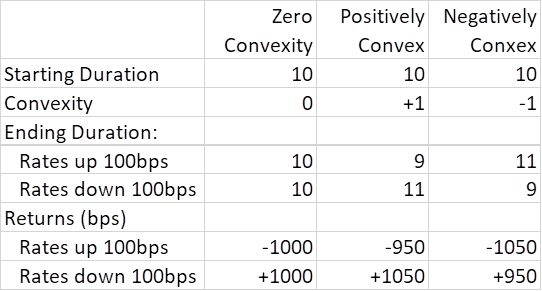
Some investors will describe convexity as the second derivative of duration. Personally, I am too far removed from my last calculus class to fully remember that the second derivative of something describes the movement of the first. So, after stripping out the confusing rhetoric, we are left with a more straightforward explanation – convexity quantifies changes in duration. Convexity tells us how much duration will move for a given change in interest rates. If the duration of the security is currently 10, and the convexity is negative one, if rates rise 100bps, the duration will move to 11. If rates fall by 100bps, the duration will drop to nine. This is a good illustration of negative convexity. Your duration rises as rates are rising.
If the convexity had been a positive one, it would have moved opposite of the direction of rates. So, if rates climbed 100bps, it would shorten to nine years over the period.
So how does this impact performance? We all know that bond prices move inversely to changes in rates. Prices rise as rates fall, and bond prices climb when rates are declining. This means you want to be adding duration in periods of falling rates and shedding duration as rates climb. For a positively convex bond, this is exactly what happens passively. The bond would shorten its duration as rates rise, thus reducing the adverse effect on its price. Or the bond will extend in duration as rates are falling, improving the upside performance for the security. So positively convex bonds result in greater price upside while softening the downside.
If the bond is negatively convex, the opposite occurs. It will extend in duration as rates climb, exacerbating the price reduction, and shorten in duration as rates fall, limiting the price upside.
In the table below, we use round numbers to highlight the changes in price and the non-linear relationship between performance and duration for a change in rates. The table also highlights the disproportionate impact on price between duration and convexity, with about 95% of the price impact coming from the former and 5% from the latter.
This should highlight the asymmetries that exist with convexity. The positively convex bond exhibits positively skewed asymmetric returns (higher highs, higher lows), while the negatively convex bond’s asymmetric return profile skews negatively (lower highs, lower lows). This is captured in the table below.
It is worth noting that despite all this negativity around negatively convex bonds, they can have their merits. Typically, the investor will receive a higher yield to bear the convexity risk. You might hear us discuss credit, structure, and price. If the credit is the same, but the convexity profiles differ, the price (yield) should typically balance the securities. If the investor expects muted volatility and thus minimal changes in duration, the investor can express this view by owning more negatively convex securities and accruing the higher yield. Having a more positively convex portfolio can be thought of as being overweight volatility. Your portfolio will (all else equal) benefit more than the index from large changes in interest rates.
*Some believe that Supreme Leader Snoke (Episode VII) is actually Mace Windu, and thus he never died.
And some extra humor:



